Describing Cellular Automata

One of the hallmarks of cellular automata is that they can be described abstractly. The rules that a system follows can be defined with relatively straightforward state-based models and functions, and the behaviors that these models describe can be applied to a variety of high-level computational frameworks and use cases.

Mathematical Models of Cellular Automata

The state of a cellular automaton at some point can be defined by:

Zs : The lattice, or the grid the game is conducted upon. In the case of the game of life, this would refer to t
S : The set of state variables for each cell.
N : The finite neighborhood, or cells related to some observed cell.
F : The transition function associated with the given rule.

The tuple (Z, S, N, F) defines the state and behavior of a given automaton based on these parameters. At each timestep increment, the states of the cells change based on the transition function.

Neighborhoods and Stability

Transition functions describe how cellular automata behave based on their neighbors. There are two major schemes used to describe neighborhoods:

Von Neumann Neighborhoods consider the neighbors of a cell to be the four cells orthogonal to it.
Moore Neighborhoods consider the neighbors of a cell to be the eight cells surrounding it.

And there are four major classes of cellular automata:

Class 1 : All cells converge to the same value.
Class 2 : Lattice converges to periodic patterns or constant structures.
Class 3 : Lattice contains seemingly random formulations with very little structure.
Class 4 : Lattice contains complex structures that propogate locally.

Class 4 cellular automata are computationally universal, meaning that they can be used to simulate any Turing machine. They are of particular interest because of their emergent behavior and variety of applications. Some major applications of cellular automata include:

Computation : Because cellular automata are distributed, parallel engines, they can be used for high-performance computations for application-specific cases.
Discrete Dynamical System Simulation : Cellular automata lend themselves to representing systems such as fluids.
Conceptual Models for Studying Patterns : The emergent behaviors of cellular automata are of deep interest to philosophers and physicists alike.

Rules and Functions

In general, the local transition function maps an lattice of cells with certain states at some timestep to a new set of cells with certain states based on the function specified by the rule and the existing states of the cells in the neighborhood of the cell under study. These functions generally take the form of conditional and logical expressions that can be implemented programmatically based on the state-based model of the automaton. For the one-dimensional case, a common framework is to define rules as a binary encoding of some decimal value, where 1 corresponds to a black square and 0 corresponds to a white square. 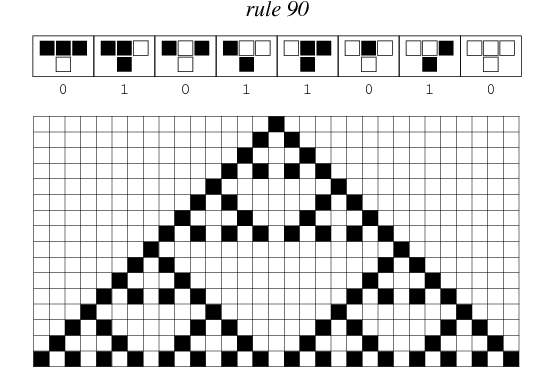For example, rule 90 would encode to 01011010, or this image: Rule 90

In two dimensions, the rules are more complicated to represent with straightforward encoding and expressions require multiple conditionals to account for the many possible cases.

Turing Machines

Turing machines are computational frameworks capable of executing some program on some input value. Universal turing machines are systems capable of simulating any arbitrary Turing machine for some program and input - such a framework is Turing complete. Generally speaking, Class 4 cellular automata are Turing complete, so they can be used to simulate any computational framework.

Emergent Behavior

Halting

At its core, the halting problem is the quesiton of whether a machine, when given an arbitrary program and input, can determine whether or not this program will finish running or run continuously. For systems that are Turing complete, the halting problem is undecidable.

The reason this is the case becomes evident by proof through counterexample. If a machine capable of solving the halting problem existed, it would, as all Turing machines do, take in both a program q and an input i - then, it could output True if the program does halt and False if it does not.

Then, we could construct an input tape that duplicates the input tape and then runs in the halting detection machine using one copy of the input as q and one copy of the input as i. If the halting program outputs False, the machine halts. If the halting program outputs True, the machine goes into an infinite loop (does not halt).

If this program is run in a Turing Machine, then it would need to continue running to return False, and it would need to stop running to return True - this is inherently self-contradictory, and proves that for any universal Turing machine there is at least one case where it cannot solve the Halting problem.

More colloquially, a program that can run infinitely would need to halt to report that it can run infinitely, so it can never report this.

The undecidability of the halting problem embodies the unpredictability of all possible cases with cellular automata : while there are certainly characterizable patterns, the behavior is unpredictable.

The Edge of Chaos

The edge of chaos is a term used to describe cellular automata where the patterns produced do not usually tend towards a completely stable state, nor do the results appear to be completely random. A cellular automata’s proximity to the edge of chaos is quantified by a parameter called \lambda, which is the fraction of a cellular automata’s rules that lead to the “life” of a cell – the edge is defined to be at or around a \lambda value of 0.5. Many of the cellular automata that have been shown to be Turing-complete, including the Game of life, have \lambda values that are close to the edge value.