Cellular Automata For Computing

---

Performance and Efficiency

Cellular automata were conceived by John von Neumann in the 1950s and originally used by him to create self-replicating systems. The system created by him was fairly complicated, with each cell able to be in one of 29 different states – since then simpler cellular automata have been explored as tools to solve other problems that are not as well served by traditional computing platforms.

Historically, cellular automata have been particularly useful in modelling, specifically in dynamic physical systems and to visualize complex pattern evolutions. Because cells in a cellular automata are only affected by their immediate neighbors, they’re useful for modelling physical systems that are only directly affected by the space adjacent to them. This tendency to only interact with neighbors also means that cellular automata can accurately model delays that are more difficult to take into account in purely mathematical descriptions, like wave propagation through space. Some other applications that show cellular automata’s use in modelling physical interactions over long periods of time include its uses in traffic modelling, studying patterns in genetics, and visualizing fluid flows.

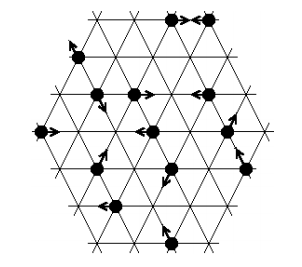
The figure below shows a Lattice Gas cellular automata that is used to model fluid flows. Each arrow represents a discrete particle in the fluid, and large-scale behaviors of the fluid can be found by looking at the average behavior of large numbers of particles.

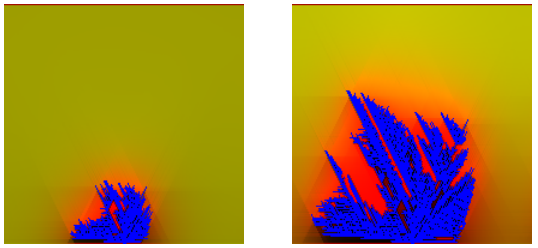
Another interesting application of cellular automata being used to model a physical system is illustrated by the figures below – students at the University of Groningen used a Boltzmann-Lattice cellular automata to model the movement of nutrients in water, then used a separate set of rules to model the growth of coral as it interacts with these nutrients.

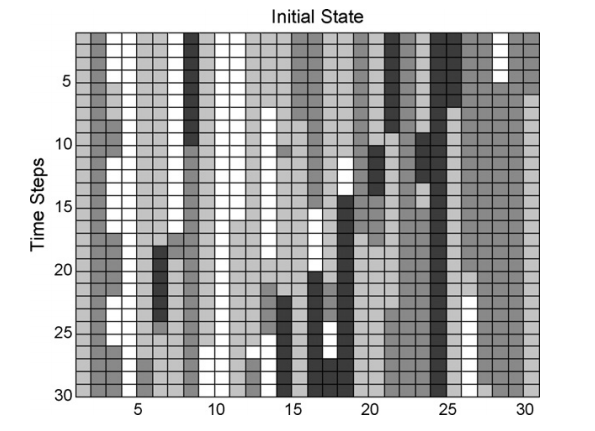
Evolution of DNA can also be modelled by a cellular automata and used to predict when mutations will occur. The figure below shows an evolution of a random DNA sequence as predicted by a cellular automata made for this purpose.

The simple rules and discrete nature of cellular automata make them better suited to these kinds of calculations than describing them with sets of equations and solving them using a traditional computing method.

At the same time, continuous operations that require direct synchrony (such as traditional logic gates) are more inefficient when implemented using cellular automata because their causal nature does not lend itself to parallelism as nicely.

Area

Comparing the differences in area between cellular automata based frameworks and traditional computing platforms is difficult because the systems are objectively in different state spaces: automata reside on a two-dimensional grid and each glider, which serves as the primary vehicle for data and energy transmission, has four discrete states that must be in phase with connections. Meanwhile, traditional computing platforms use tightly-packed transistors as the medium to move electrons, which have two discrete states. As a result, both systems present unique advantages and drawbacks in particular use cases: likening a transistor to a cell presents a highly inefficient model, but when representing complex rule sets for cell behavior, cellular automata are much simpler.